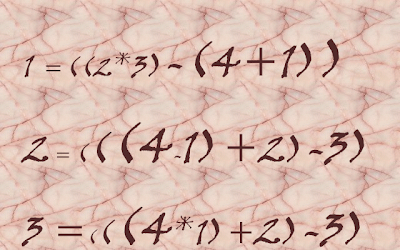Bowling Pin Arrangement Puzzle

Once you went to bowling with your friend. All the bowling pins were labelled with different integer from 0,1,2 .. to 9. The arrangement of pins (in a triangle form) was very interesting. If two pins are side-by-side, the sum of their labels (reduced modulo 10) is equal to the label of the pin in front and between them. For Example

1   2   4   5

  3   6   9

   9   5

   4

Expressing Numbers with Number Puzzle

We are given four integers 1, 2, 3 and 4 to express other numbers with an arithmetic expression using these numbers exactly once and the mathematical operators +,-,* (addition, subtraction, multiplication).  For example 1 can be represented as 1 = (2*3)-(4+1). The arithmetic operation can be used zero or multiple times but the digits(1, 2, 3, 4) should be used exactly once. So an expression to represent 1 = 2+3-4 is not valid. Where as 10 = 1+2+3+4 is a valid expression to represent 10. Also you are allowed to reuse operators (such as 24 = 1*2*3*4) and you are allowed to put '(', ')' at any desired position to change the precedence of evaluation.  But you are not allowed to join digits together such as (12+34).

Sequence of Equations Puzzle

This is a simple yet tricky puzzle. It seems this puzzle has been solved by pre schoolers in an average 10 Mins. By entry level programmers in around 30 Mins. And strangely people good in mathematics have taken more time to solve this riddle. Check which category you belong to. If you get the answer simply post the value in comment section. Within a day or two I will post the explanation. 

Numbering the CDs Puzzle

A friend of mine works in a data management company and he needs to compulsively records  all the backuped data on CD Roms. To this end, he has a huge collection of CD ROMs. He has long given up on trying to label these cassettes with any meaningful names. Now he just numbers them and maintain the description based on number given to CD else where. The numbers go from 1 up and are consecutive.

The Golf Score Puzzle

Three friends Andrew, watson and Lestrade were playing Golf. Andrew made three statements regarding their scores for a particular round. Can your work out their individual score??

Prisoners and The Switch Room Puzzle

A prison jailor meets with the twenty three convicts when they arrive at the prison. He tells them:

You may meet today to discuss and plan a strategy, but after today you will be locked in isolated cells and have no communication with one another.

There is in this prison a "switch room" which contains two light switches, labeled "A" and "B", each of which can be in the "on" or "off" position. I am not telling you their present positions. The switches are not connected to any appliance. After today, from time to time, whenever I feel so inclined, I will select one prisoner at random and escort him to the "switch room", and this prisoner will select one of the two switches and reverse its position (e.g. if it was "on", he will turn it "off"); the prisoner will then be led back to his cell. Nobody else will ever enter the "switch room".

Ten Assertions Puzzle

Fill in the blanks with numbers so that all the statements are true.

Number of occurrences of the digit 0 in this puzzle is  _____.
Number of occurrences of the digit 1 in this puzzle is  _____.

Number of occurrences of the digit 2 in this puzzle is  _____.

Number of occurrences of the digit 3 in this puzzle is  _____.

Number of occurrences of the digit 4 in this puzzle is  _____.

Number of occurrences of the digit 5 in this puzzle is  _____.

Number of occurrences of the digit 6 in this puzzle is  _____.

Number of occurrences of the digit 7 in this puzzle is  _____.

Number of occurrences of the digit 8 in this puzzle is  _____.

Number of occurrences of the digit 9 in this puzzle is  _____.

The Bulb Puzzle

There are 100 light bulbs lined up in a row in a long room. Each bulb has its own switch and is currently switched off. The room has an entry door and an exit door. There are 100 people lined up outside the entry door. Each bulb is numbered consecutively from 1 to 100. So is each person. Person No. 1 enters the room, switches on every bulb, and exits. Person No. 2 enters and flips the switch on every second bulb (turning off bulbs 2, 4, 6, …). Person No. 3 enters and flips the switch on every third bulb (changing the state on bulbs 3, 6, 9, …). This continues until all 100 people have passed through the room.

What is the final state of bulb No. 64? And how many of the light bulbs are illuminated after the 100th person has passed through the room?