Euler Constant
When I read about logarithm for first time in High school I
understood as it as “The logarithm of a number is the exponent to which a base(usually 10) must be raised to produce that number”
For example, the logarithm of 1000 to base 10 is 3, because
1000 is 10 to the power 3: 1000 = 10 ×10 ×10 = 103. More generally, if x = by,
then y is the logarithm of x to base b, and is
written y = logb(x), so log10(1000)
= 3. This was quite reasonable to understand.
More recently while studying complexities
of algorithm, studying Trees/Graphs and studying limits of computer numbers(being
represented by ‘0’ and ‘1’) the preferred base for any logarithm function has
been ‘2’. This is also reasonable considering any number in computer world is
nothing but 0s and 1s and working with ‘2’ as base makes the calculation
easier.
But then there was a brief phase when I
studied calculus and I came across Euler Mathematical constant ‘e’. ‘e’ is an
irrational number approximately equal to 2.71. I could not understand the
motivation behind using such a number as base for any logarithm. It was first
used by Euler. He was a great mathematician and there should have been a
genuine reason on using this constant as base for natural logarithm.
I am sure many of you have also given a
thought to it. Thanks to Internet and you tube, today I have luxury of reading
and listening to some of the great mathematicians and professors of the world. Hence I looked on web trying to find out the answer and here is what I discovered. I was totally amazed by power of this mysterious constant ‘e’ and more
importantly ex. A book called ‘CALCULUS’ by
professor Gilbert Strang from MIT has explained it very beautifully. The professor is very generous to upload one of his lecture videos on the web as well. Some of
the formulae and pictures in this post are taken directly from his book.
The use fullness of ‘e’ comes from the
method of finding slope of function which is of the form bx for example 2x, 3x,10x or pix etc. Any function of this form
is called exponential function and its slope is defined by its derivative
dy/dx. The inverse of the function bx is logbx.
We call these
functions inverse of each other because if we take y = g(x) = bx and
x = g(y) logb y, then the inverse rule will apply ie
After introducing these two functions let’s try
to find their derivatives. The definition of derivative of a function is limit
of ΔY/ ΔX. Lets apply to function bX
So here c is the mysterious constant. So if we make this
mysterious constant 1 with proper selection of base b, we will get an amazing
result with respect to exponential function. And that is the motivation behind
using ‘e’ as base ’b’.
For deriving at the value of e, lets take an special case
of x = 0 or y = 1. We know that b0 = 1 and logb1 = 0.
Applying this special case we find that the derivative or slope of bx at
x=0 is ‘c’ and slope of logby at y=1 is 1/c. With right choice of
base those slope can be equal to ‘1’. Applying the derivative formula at y=1 directly we
get:
The quantity (1 + h)1/h is unusual, to put it
mildly. As h à
0, the number 1 + h is approaching 1. At the same time, l/h is approaching
infinity. In the limit we have 1∞. But that expression is
meaningless (like 0/0). Everything depends on the balance between "nearly
1" and "nearly ∞." This
balance produces the extraordinary number e
Definition:
Number ‘e’ is equal to:
So when base b is e then the constant c = logee
= 1.
And that’s the reason to select e
as base for all logarithmic functions in calculus.
There are several ways to calculate the numerical value of
‘e’. It is equal to 2.718.. Since it’s an irrational number one can never find
its exact value but around 125 000 digits of e are found. The table below shows
a method of approximately finding e.
‘e’ make exponential function so peculiar that the function ex is same as its slope. This is the only know function to exhibit this property. ‘e’ can be alternatively defined as following:
Further Reading
As mentioned earlier I have collated the contents for this post from one of the MIT open courses. In case you want to learn more about exponential function and 'e' then watch the following video.
Other course contents can be found at this link
Summing Up
In this post I have tried to explain how 'e' come into existence and why using it reduces complexity of several Calculus arithmetic. How ever there are several other fields in which natural logarithm is preferred. As per wiki following table summaries the various scenarios in which 2,e and 10 are used as preferred bases.
Take care..
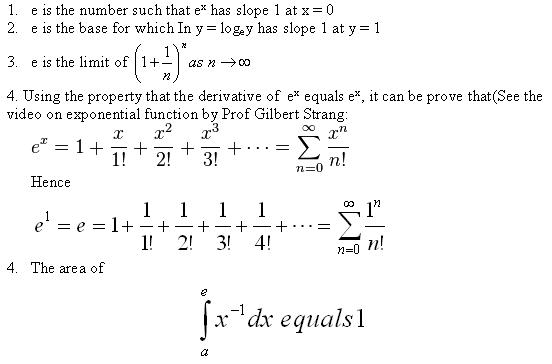
No comments:
Post a Comment